| �P�D���[�N��R |
�@�@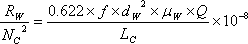 |
�m���^T2�n |
|
|
| �Q�D���[�N���A�N�^���X |
�@�@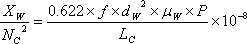 |
�m���^T2�n |
|
|
| �R�D�R�C�����A�N�^���X�y�ђ�R |
�@�@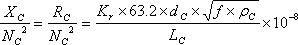 |
�m���^T2�n |
|
|
| �S�D�G�A�M���b�v���A�N�^���X |
�@�@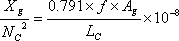 |
�m���^T2�n |
|
|
| �T�D�O�������ɂ�郊�A�N�^���X |
�@�@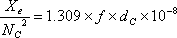 |
�m���^T2�n |
|
|
| �U�D���A�N�^���X���v |
�@�@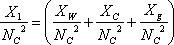 |
�m���^T2�n |
|
|
| �V�D���[�N������R |
�@�@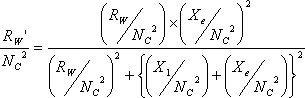 |
�m���^T2�n |
|
|
| �W�D�S���A�N�^���X |
�@�@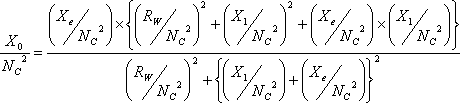 |
�m���^T2�n |
|
|
| �X�D�S��R |
�@�@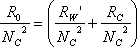 |
�m���^T2�n |
|
|
| �P�O�D�R�C������ |
�@�@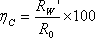 |
�m%�n |
|
|
| �P�P�D�C���s�[�_���X |
�@�@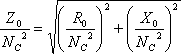 |
�m���^T2�n |
|
|
| �P�Q�D�R�C���͗� |
�@�@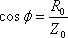 |
�m-�n |
|
|
| �P�R�D�R�C������d�� |
�@�@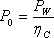 |
�mkW�n |
|
|
| �P�S�D�R�C���瑊�d�� |
�@�@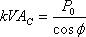 |
�mkVA�n |
|
|
| �P�T�D�R�C���d�� |
�@�@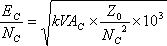 |
�mV/T�n |
|
|
| �P�U�D�R�C���A���y�A�^�[�� |
�@�@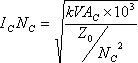 |
�mAT�n |
|
|