発行者からのお願いです。
(1)このメルマガで記述する技術的内容は、何物をも保証するものではありません。
従って、誤った記述に伴う、物的、人的損害には責任を負えませんので、ご了解下さい。
(2)このメルマガの著作権は、発行者にあります。
無断転用をご遠慮願います。
◇◇◇◇◇◇VOL-4「高周波誘導加熱の原理(その2)」◇◇◇◇◇◇
約半年間、メルマガの発行が途切れてしまい、読者の方にご迷惑をおかけしました。
今後は、出来るだけ、1ヶ月〜2ヶ月に1回は、発行していきたいと思います。
ホームページ:http://www.eguchi-hf.co.jp.
前回に引き続き「高周波誘導加熱の原理」について考えて見ます。
前回、説明しましたように、
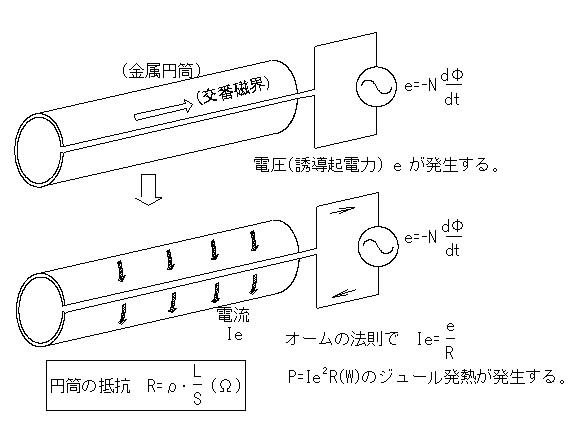
コイルに流れる電流が交流であると、金属円筒に鎖交する「磁界が変化」するので、金属円筒に電圧が誘起されます。
円筒のどの間に電圧が発生するのか、疑問になりますが、円筒の一端が切れた部分に電圧が発生すると考えると理解しやすくなります。
図のように円筒の一端が切れた部分に、「e=-N・dΦ/dt」の交流電圧が発生します。
円筒が一回巻きなので、巻数Nは1となります。
金属円筒の材質・大きさで決まる抵抗Rによって、オームの法則で決まる電流Ieが円筒に流れます。
抵抗のある円筒に電流が流れることで、Ie×Ie×R(ワット)の発熱で、金属円筒が加熱されます。
なお、オームの法則、円筒の抵抗は、分かりやすくするため、直流の概念で記述していますので、
交流を扱う実際の高周波誘導加熱では、複雑な式になります。

今回は、上記の現象をもう少し詳しくみていきたいと思います。
今、図のように、厚さ1mm、直径50mm、長さ200mmのステンレスの円筒が加熱コイルの中にあったとします。
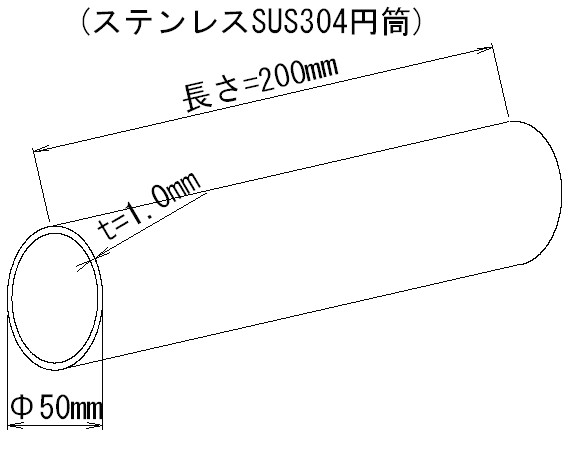
このとき、加熱コイルに流れる電流で発生した磁界の変化によって、ステンレスの円筒に2ボルト(V)の交流電圧が発生(誘起)したものとします。
電圧e(V)と、円筒の抵抗R(Ω)が分かると、円筒に流れる電流Ie(A)は、オームの法則によって求められます。
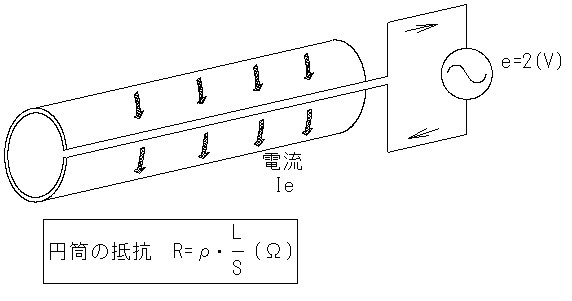
円筒の長さLと、断面積Sは、下記のようになり、
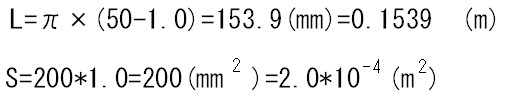
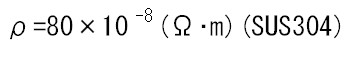 とすると、
とすると、
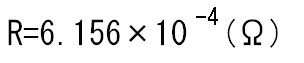 となります。
となります。
よって、ステンレス円筒に流れる電流Ie(A)と、円筒の発熱量P(kW)は、
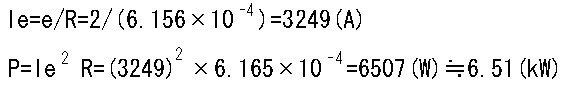
となります。
誘起電圧が、たったの2(V)なのに、6.5(kW)の発熱量を得ることが出来ます。
また、この発熱量は、流れる電流の二乗に比例するので、誘起電圧の二乗に比例することになり、
発生する磁界、すなわち加熱コイルに流れる電流を制御することで、被加熱物の発熱量を、容易に、しかも瞬時に変えることが出来ます。
高周波誘導加熱に関する基礎的な話を出来るだけわかりやすく、不連続テーマ・不定期発行のメルマガで進めてまいります。
ご質問は、こちらまで:メール